Advent of Code 2024: Day 14

Advent of Code is a advent calendar where programmers compete to solve challenges each year in order to improve their skills or just to have fun. Since the start of December, I've been working each day on solving these myself.¹ Normally, my solutions are nothing of note and are similar to many others. Today, the 14th day, it feels almost as if everyone has their own completely different solutions. So I felt it was a perfect time to write up a post on here to explain mine.

Part One

For part one, it explains how there's a list of robots each with a initial position and velocity. These robots are inside a room of 101 units wide and 103 units tall. The input data for today is the robots and they were formatted as such:

content_copyp=0,4 v=3,-3
p=6,3 v=-1,-3
p=10,3 v=-1,2
p=2,0 v=2,-1

So the first line is a robot with a starting position of (0, 4) and a velocity of (3, -3). After 2 seconds, the robot would be at (6, -2) but since that would be outside the room on the y, it wraps around to the bottom to (6, 101).

A safety factor can be measured from how many robots are in each of the four quadrants split down the middle after some amount of seconds. It asks for the safety factor after 100 seconds as the answer for part one.

The most obvious solution is to step through each second and move every single robot one by one. This would have a time complexity issue with how seeing further into the future would take longer to calculate. Previous days had me spooked about this, so I decided to go for an algorithm that doesn't take longer with more seconds.

Really all we care about is the final positions of each robot. Instead of stepping through each second, we can find out the total move distance and then wrap it within the room's bounds. Let's say we have a robot starts off at (0, 0) and it moves (1, -2) every second. At 10 seconds, the total move distance is (10, -20). Now we need to restrict this to the bound's of the room. At first I was going to use the modulo operator which is often described as the remainder operator. There are some key differences between these that leads to undesired outcomes.

content_copylet x = 10 % 101;  // x = 10
let y = -20 % 103; // y = -20

The modulo operator works just fine in the positive direction, but it fall apart in the negative. It would still wrap around, but it wrap at -103 instead of at zero. I did some digging and found Rust has a function just for what I need; it's called the euclidean remainder.

content_copylet x = 10.rem_euclid(101);  // x = 10
let y = -20.rem_euclid(103); // y = 83

Now, we are able to get the final position after any amount of time with constant time complexity. Next, we need to map those final positions to a quadrant and calculate the safety factor. This worked out pretty well and was able to give me the solution for part one.

Part Two

For part two, I was expecting something along the lines of where all the bots would be after a couple billion seconds. I couldn't have been further from what part two needed from me. when the prompt loaded, it was short and very scary. All it told me was that there was some hidden image of a Christmas tree found after some amount of time. It asked for the number of seconds until the bots form the tree. All the optimizations I made in order to speed up part one would have little to no affect on the speed of this since I would have to check each and every second.

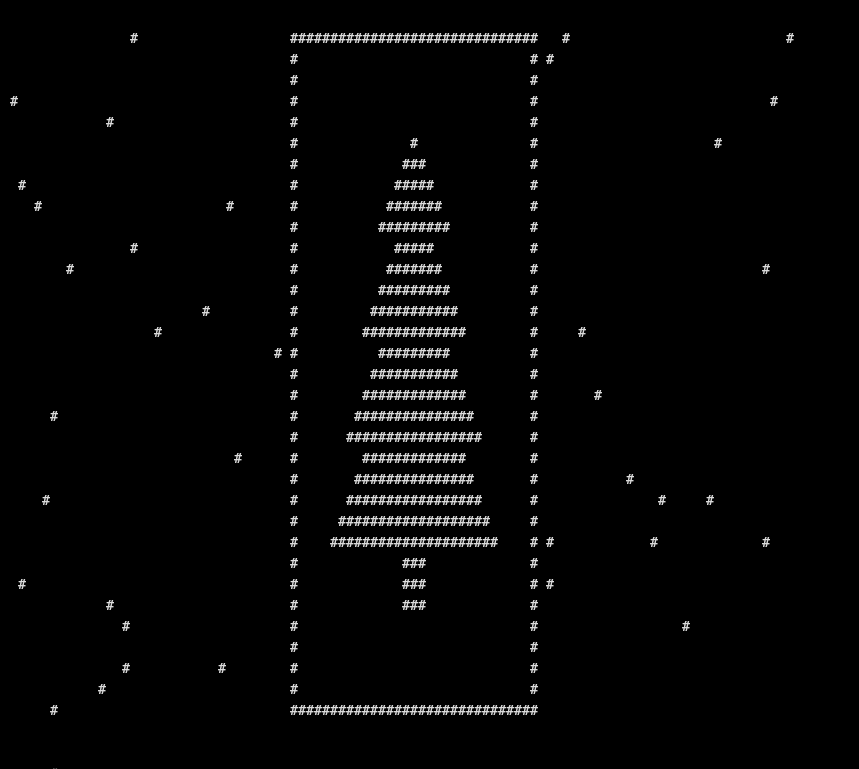
First we need to figure out what patterns to look for. My first though was to manually step through a see if I could find any myself. I created a simple print function that let me step through each second. After a bit of searching, it turned from random noise into this:

This told me that the tree Easter egg was most likely centrally located on the x. I would need to get a value to describe this. My first though was to get the standard deviations of the x. A lower deviation would say that many bots are close to each other. I implemented the standard deviation formula from online and plugged it into my code. Then, I found the deviation of the image from before and it was 18 units. So I just filtered the printouts to only be seconds where it was 19 or lower (giving some wiggle room). After some manual searching for a few moments, I found the tree:

This gave me the answer, but I still wanted to make it fully automatic. Something I did notice though is how the height is also very central which means I can do further filtering by additionally calculating the y derivations. After adding the same checks for the y, the first image was the correct answer. Now we can get rid of the printing and have the computer do all the work.

A Retrospective

I really enjoyed today's puzzle. Many people didn't like how vague part two was, but I fell that was one of the best parts. A big part of today was finding out the key characteristics of the image you needed to be looking for. Only after you figure these out can you solve the puzzle. I also find it interesting how many different ways people came up with solving this; from entropy algorithms to even Windows Explorer, people were able to solve today. I hope more days are like this one.